重复测量分析的完整思路

repeated measures analysis

我们昨天刚发完MMRM的文章，在星球里，就有小伙伴问到下面这个问题。

对于这个问题，我们要从重复测量分析说起。

所谓重复测量分析，是指在同一个受试者上，对同一个endpoint进行多次测量，比如，我们在一个RCT中，对受试者的血压进行了多次测量，这就是重复测量。重复测量的数据，一般是longitudinal data，也就是纵向数据，每个受试者的测量数据是一个时间序列。一旦在同一个人身上出现了测量的时间序列，特别需要注意的东西就来了：测量间的相关性问题（correlation structure）该如何考虑？

重复测量方差分析

对于这个测量间相关性问题，我们大家很常见的处理方法是重复测量方差分析（repeated measures ANOVA）。

对于repeated measures ANOVA，我们将处理组间的效应作为固定效应，而将time效应作为blocking factor，这样，我们就可以借助two-way anova，估计出组间的效应，以及组间的效应是否随着时间的变化而变化。但是，two-way anova的一个假设是，观测间必须独立。在重复测量数据中，不同时间节点不同subject的测量是独立的，但是同一subject的测量间不独立，这时候，我们需要将每组中的subject效应单独考虑，并对同一subject间测量的相关性做出一定的假设。这样，我们就在重复测量方差分析中引入了treatment effect、subject (within group) effect、time effect以及可能的treatment-time-interaction。

这个方法的优点是简单，缺点是，对于测量间的相关性，我们有且只有能够做出一种假设，即compound symmetry，也就是说，我们假设所有的测量间的相关性都是一样的。

很好理解的假设对吧，但是这个假设在实际很多情况下都是不成立的，比如，我们在一个RCT中，对受试者的血压进行了多次测量，我们假设第一次测量和第二次测量间的相关性与第一次测量和第三次测量间的相关性是一样的，此时，这个假设就是不成立的，因为，血压第一次测量和第二次测量的相关性肯定比第一次测量和第三次测量的相关性要高。所以，重复测量方差分析的缺点就是，对于测量间的相关性，我们只能做出一个假设，并且这个假设在很多情况下是不成立的。

在SAS中我们可以借助glmproc步来完成two-way anova。下面是一个例子。

proc glm data = discom;
  class vacgrp pat visit;
  model score = vacgrp pat(vacgrp) visit vacgrp*visit/ss3;
  random pat(vacgrp);
  test h=vacgrp e=pat(vacgrp);
quit;
run;

mixed-effects modelling

相比于来自于ANOVA的重复测量方差分析，现在有很多基于general linear modeling techniques的混合效应模型方法。这些方法在SAS中可以分别通过mixed、glimmix、genmod等proc步来实现。这些方法都有一个共同点，即，可以适应处理missing的情况，并且针对correlation structure，有丰富的假设可供选择考虑。下面我们就来分别介绍下。

线性混合效应模型（linear mixed-effects model or linear mixed model）是广义线性模型（general linear model）的拓展。GLM假设random errors是独立且正态分布，LMM则可同时包含固定效应、随机效应在内，同时允许对random errors做灵活的协方差矩阵的假设。相比于GLM，LMM由于可以应对复杂的random errors（甚至erros with heterogeneous variances），因而主要用于处理longitudinal和hierarchical数据。其中，针对continuous data，mixed model repeated measures（MMRM）主要就是用来处理重复测量数据的分析，这部分我们在昨天的文章中已经介绍过了；针对categorical或者count data，generalized linear mixed-effects model（GLMM）主要用于这部分数据的分析。对于LMM、GLMM和MMRM，你可以理解为虽然三者都是mixed-effects modeling，但是侧重点不一样：MMRM主要就是重复测量数据，GLMM主要是endpoint的形式灵活，而LMM相对于MMRM的应用更加广泛，不局限在重复测量。

我们比较LMM和上面的repeated measures ANOVA，LMM可以采用多种相关性假设：unstructured (UN)、homogeneous Toeplitz (TOEP)、auto-regressive (AR(1))、heterogeneous auto-regressive (ARH(1))、compound symmetry (CS)、heterogeneous compound symmetry (CSH)等，这个我们昨天在MMRM中已经提到过。

下面是一个例子。

proc mixed data = discom;
  class vacgrp pat visit;
  model score = vacgrp visit vacgrp*visit;
  repeated visit / subject=pat(vacgrp) type=un; 
  title "PROC MIXED with Unstructured Covariance";
run;

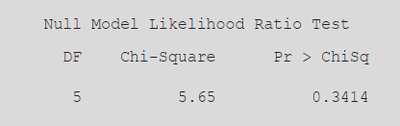
SAS中会有一个null model likelihood ratio test，用来检验是否需要考虑random effects，如果p值小于0.05，则说明需要考虑random effects。需要注意的是，这个检验是针对random effects的，而不是针对correlation structure的。

generalized estimating equations

generalized estimating equations（GEE）同样是用于分析重复测量数据的另一种方法，它同样基于specify重复测量间的相关性（working correlation），但是和上述方法不同的是，它更加robust，即使错误指定了相关性矩阵，它仍然能有较好的模型参数的输出，比上述方法更加稳定。GEE不依赖相关性矩阵的正确指定，但是上述其他方法需要。另外，需要注意的是，GEE的输出是针对population的，而不是针对individual的，这一点和上述的方法不同。

下面是一个例子。

proc genmod data = unialz;
  class treat month pat;
  model adascog = treat month treat*month / type3;
  repeated subject = pat / type = ar(1);
  title "Autoregressive Correlation (AR(1)) Working Correlation";
run;

此外，LMM对于缺失机制的假设是基于MAR，而GEE的缺失假设MCAR更加严格。而在实际数据分析中，实际上这两种假设都是不可知正确与否的，在这种情况下，填补之后再做敏感性分析就能最大程度上提升结果的可信度。

最后，欢迎大家进入我们的星球提问交流。

Did you find this page helpful? Consider sharing it 🙌