LSTM参数数量的计算

LSTM

我们前面发过这篇RNN的pytorch实现，在里面提到了，RNN会出现梯度爆炸/消失的问题，而LSTM可以解决这个问题。

LSTM的全称是long short-term memory，是一种特殊的RNN，其结构如下图所示。

实际上，相比于RNN，LSTM引入了门控机制，有三个门（gate）：forget gate，input gate，output gate。门控机制的引入控制了信息传递的路径，从而解决梯度爆炸/消失的问题。具体来看，如下图。

$f_t$是forget gate，$i_t$是input gate，$o_t$是output gate，$c_t$是cell state，$h_t$是hidden state，$x_t$是输入，$W$是weight，$b$是bias。

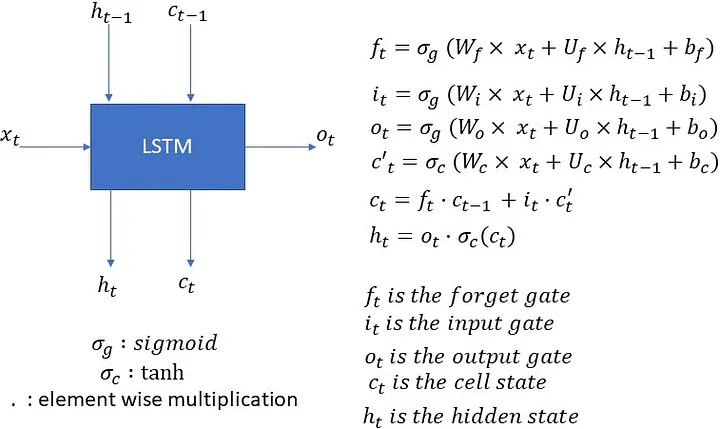
LSTM将历史信息看作一种记忆，在简单循环网络中中，记忆是通过hidden state来传递的，然而，hidden rate在每个时刻都会被更新，因此，记忆会随着时间的推移而消失，我们将其看做一种短期记忆。而在LSTM中，记忆是通过cell state来传递的。cell state有能力将关键信息保存一定的时间间隔，同时，其保存信息的生命周期要长于短期记忆，但又短语长期记忆，因而这就是LSTM名字的由来。

更加具体的，如上图，cell state可以看作是一个管道，信息可以从管道中流过，也可以从管道中流出，这个过程是通过门控机制来控制的。forget gate控制信息从管道中流出的比例，这是由sigmoid激活函数进行控制；input gate则控制当下时刻输入信息对cell state的更新比例，output gate则控制更新后的cell state信息从管道中流出的比例。

LSTM借助这种软性的门控机制，可以有效的解决梯度爆炸/消失的问题，从而可以有效的处理长序列数据。

LSTM参数数量的计算

接下来我们来看LSTM参数数量的计算。

在上面第二张图的公式中，我们已经可以清楚地看到，在一个LSTM cell中，上面四个函数各有一个W、U矩阵，分别对应于输入、隐藏状态的权重，那我们就可以计算这些权重矩阵的维度，即$hidden_{size} \times input_{size} + hidden_{size} \times hidden_{size}$，这些矩阵都是可训练的，此外，每个函数都有一个偏置矩阵，维度为$hidden_{size}$，因此，这些矩阵的数量就是LSTM的参数数量，由于存在四个函数，则总的参数数量为$$4 \times (hidden_{size} \times input_{size} + hidden_{size} \times hidden_{size})+ hidden_{size}$$

我们利用一个小的代码示例来验证一下这个公式。

input = Input(shape=(30, 3))
output= LSTM(2)(input)
model_LSTM = Model(inputs=input, outputs=output)

model_LSTM.summary()

可以看到，和公式的结果保持一致。

Did you find this page helpful? Consider sharing it 🙌