置信区间的报告

置信区间与p值

统计检验的p值以及相关统计量的置信区间已经成为论文发表报告的必备选项。但是相比于p值的流行，置信区间的使用率相对较低。

置信区间是对参数估计的一种区间估计，它提供了对参数估计的不确定性的度量。在统计推断中，置信区间是一种更加全面的统计量，它不仅提供了参数估计的点估计，还提供了参数估计的区间估计。在实际应用中，相比于p值单纯地接受或拒绝原假设，置信区间提供了更多的信息，可以帮助研究者更好地理解数据，更好地解释研究结果。

ICH Harmonized Tripartite Guideline on statistical principles for clinical trials关于CI的说明是：

Estimates of treatment effects should be accompanied by confidence intervals, whenever possible, and the way in which these will be calculated should be identified…. it is important to bear in mind the need to provide statistical estimates of the size of treatment effects together with confidence intervals (in addition to significance tests).

置信区间

我们在实际论文和项目中，应当习惯性地使用并报告置信区间。一般地，两种常用的置信区间分别是基于一定分布的置信区间和基于非参数方法的置信区间。对于基于正态分布的置信区间，常用的有t分布置信区间和Z分布置信区间。对于基于非参数方法的置信区间，常用的有bootstrap置信区间和distribution-free置信区间。

两种类型的选择主要取决于对确定参数分布的信心。对于不能较好拟合数据的情况，使用非参数方法更为合适。但是也要注意，非参数CI可能会比参数方法CI更宽，因此在报告时需要进行解释。某些时候，非参数CI也可能不存在。

在SAS中，CI的计算已经非常方便，这里举例对于proportions或percentages的参数CI计算。

proc freq data=&ind noprint;
	table &trt*&var /chisq riskdiff;
	output out=pval PCHI rdif2;
data pval; 
	set pval; 
	length categ $55.;
	categ="&cat";
	pv=P_PCHI;
	ll=100*L_RDIF2;
	ul=100*U_RDIF2;
	keep pv ul ll categ;
run;

对于distribution-free置信区间的计算，这里举例对于median的非参数CI计算。

ods listing close;
ods output quantiles=pctldf ;
proc univariate data=final loccount
	modes cibasic(alpha=.05)
	cipctldf(TYPE=ASYMMETRIC
	alpha=.05);
	var P&var ;
	by &trt ;
run;
data pct; 
	set pctldf;
	if quantile='50% Median' ;
run;
ods output close;
ods listing ;
data _null_ ; 
	set pct; if &trt= "&trt1";
	call symput ('lclddf',
	put(LCLDistFree, 7.2));
data _null_ ; 
	set pct; if &trt= "&trt1";
	call symput ('uclddf',
	put(UCLDistFree, 7.2));

置信区间与p值的解释

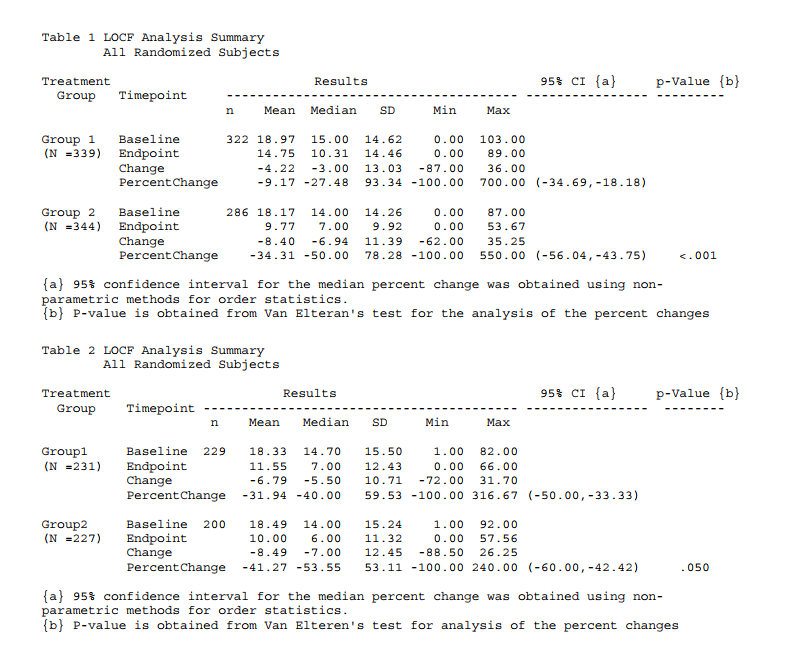
如Table 1 van Elteren’ test，CI和p值的结果一般是一致的，但是p值无法直接反映多大的效应量，这时候，CI就能更加直观地反映两组之间不重叠的参数范围。但是，当二者结果不一致的时候，如Table 2的结果，p值为0.05，但是CI重叠了，这时候，CI的结果能更加直观地反映了两组之间的差异的不确定性。我个人还是比较倾向于选择CI的结果。

相关代码已经放进了星球里。

Did you find this page helpful? Consider sharing it 🙌