RCT中治疗效应估计的不同方法对比

治疗效应的估计方法

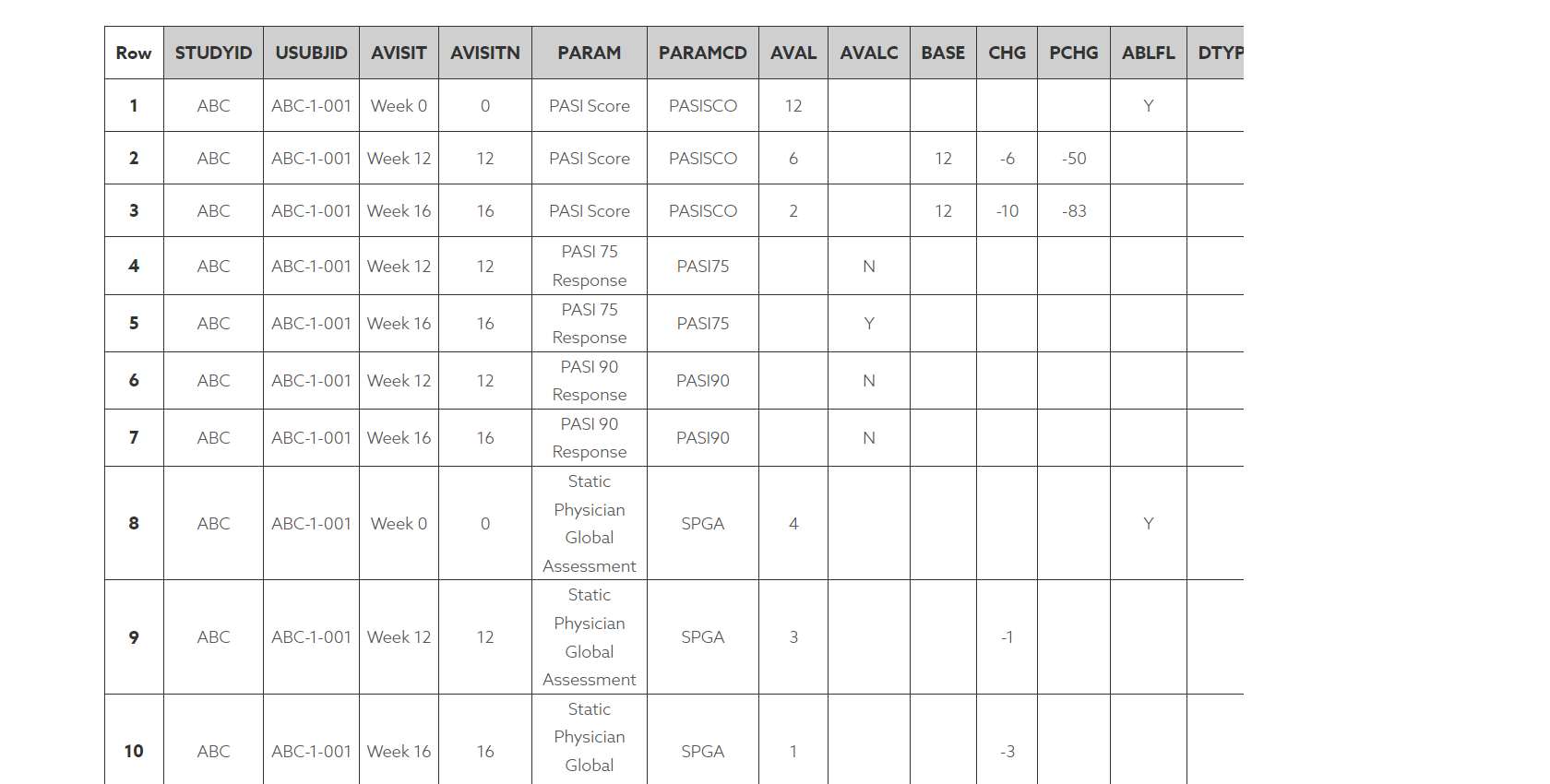
在随机对照试验（RCTs）中用于估计治疗效应的统计方法主要有三种：纵向协变量分析（Longitudinal analysis of covariance）、重复测量分析（Repeated measures）和变化分析（Analysis of changes）。我们首先来分别介绍下。

纵向协变量分析

纵向协变量分析方法通过调整结果变量在不同随访测量时间点的基线值来估计治疗效应。

所需的数据结构为：

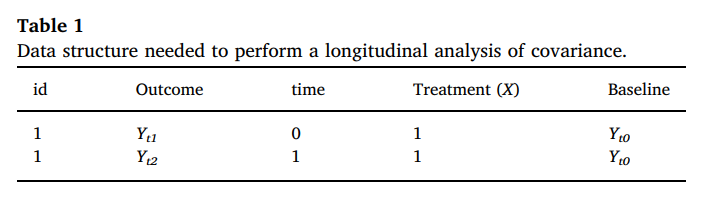
公式为：

$$Y_{t} = \beta_0 + \beta_1X + \beta_2Y_{t0}$$

由于调整了不同trt组的基线值，因此纵向协变量分析方法能够更好地估计治疗效应，是我们比较推荐的方法。

上面这个公式估计的是总的治疗效应（即treatment effect on average over time），当我们需要估计不同随访时间点时的治疗效应时，我们可以在模型中加入随访时间及trt与随访时间的交互项来估计，公式为：

$$Y_{t} = \beta_0 + \beta_1X + \beta_2Y_{t0} + \beta_3time + \beta_4X\times time$$

重复测量分析

重复测量分析方法则利用所有随访测量的结果变量值进行分析，但未对基线差异进行调整。

所需的数据结构为：

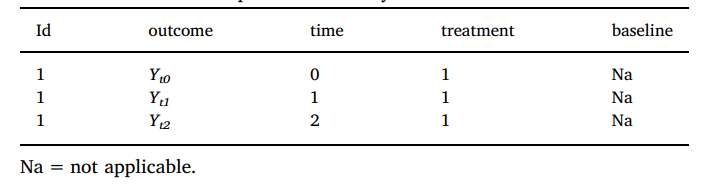
估计总体治疗效应的公式为：

$$Y_{t} = \beta_0 + \beta_1X + \beta_2time + \beta_3time\times X$$

注意，由于是估计总体效应，其中时间变量为连续性变量时，基线时间需要code为0，非基线需要code为1。

当需要估计不同随访时间点时的治疗效应时，我们同样可以在模型中加入随访时间及trt与随访时间的交互项来估计，公式为：

$$Y_{t} = \beta_0 + \beta_1X + \beta_2dummy_time_1 + \beta_3dummy_time_2 +\ \beta_4dumm_time_1\times X + \beta_5dummy_time_2 \times X$$

两者的区别在于时间变量为连续性变量还是dummy出来的分类变量。

问题就来了：为什么不调整基线值呢？因为在重复测量分析中，我们假设了随访时间点的测量值是独立的，因此不需要调整基线值。但是，这个假设在实际中往往是不成立的，因此重复测量分析方法估计的治疗效应往往是高估的。

为了在重复测量分析中调整基线值，我们将公式分别修改为：

$$Y_{t} = \beta_0 + \beta_1time + \beta_2time\times X$$

$$Y_{t} = \beta_0 + \beta_1dummytime_1 + \beta_2dummytime_2 + \ \beta_3dummytime_1 \times X + \beta_4dummytime_2 \times X$$

同学们会发现，此时公式中单独的trt项已经不再存在，而是被纳入到$\beta_0$中，此时治疗效应的估计来自trt与时间交互项的系数。这样调整以后，经过模拟研究发现，此时重复测量分析方法估计的治疗效应与实际情况更为接近。

变化分析

变化分析，顾名思义，是通过计算随访时间点相对于基线的变化值来估计治疗效应。

所需的数据结构为：

公式分别为：

$$Y_{t} - Y_{t0} = \beta_0 + \beta_1X$$

$$Y_{t} - Y_{t0} = \beta_0 + \beta_1X + \beta_2 time + \beta_3X \times time$$

即使是去掉了基线值，模拟研究发现，变化分析方法忽略了基线值，导致了治疗效应的低估。

同样的问题，我们还是同样需要在模型中调整基线值：

$$Y_{t} - Y_{t0} = \beta_0 + \beta_1X +\beta_2Y_{t0}$$

$$Y_{t} - Y_{t0} = \beta_0 + \beta_1X + \beta_2 Y_{t0} + \beta_3X \times time$$

此时估计出来的治疗效应与实际情况更为接近。

方法推荐

研究文献表明，纵向协变量分析方法估计的治疗效应与调整基线的变化分析方法更为接近。

从数学公式上看，我们也能得到这个结论。

因此，在选择分析方法时，需要考虑不同方法对治疗效应估计的影响，以确保结果的准确性。

SAS代码已经放进了星球里。

Did you find this page helpful? Consider sharing it 🙌